Получили четырехугольники ABB1A1, BCC1B1, CDD1C1, DAA1D1. Рассмотрим один из этих четырехугольников. Например, четырехугольник ABB1A1. Стороны AA1 и BB1 параллельны по условию. По свойству параллельных плоскостей стороны AB и A1B1 параллельны. То есть, четырехугольник ABB1A1 – параллелограмм, аналогично, параллелограммами будут каждый из четырехугольников BCC1B1, CDD1C1, DAA1D1.

Поверхность, составленная из двух равных параллелограммов ABCD и A1B1C1D1 и четырех параллелограммов ABB1A1, BCC1B1, CDD1C1, DAA1D1называется параллелепипедом и обозначается так: ABCDA1B1C1D1

Параллелограммы, из которых составлен параллелепипед, называются гранями.

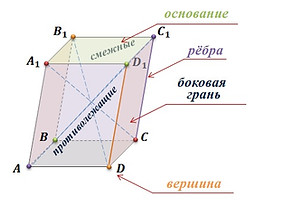
На рисунке изображен параллелепипед ABCDA1B1C1D1. Обратите внимание, все шесть граней параллелепипеда – параллелограммы.

Стороны параллелограммов называются ребрами параллелепипеда, а их вершины – вершинами параллелепипеда. Две грани параллелепипеда называются противолежащими, если они не имеют общего ребра. Например, грани AA1B1B и DD1C1C – противолежащие.

Грани имеющие общее ребро называются смежными. Например, грани AA1D1D и DD1C1C – смежные, ребро DD1 у них общее.

Иногда какие-нибудь две противолежащие грани параллелепипеда выделяются и называются основаниями, тогда остальные грани – боковыми гранями, а их стороны, соединяющие вершины оснований параллелепипеда, - его боковыми ребрами. В нашем случае у параллелепипеда ABCDA1B1C1D1 грани ABCD и A1B1C1D1– его основания. Остальные же грани являются боковыми гранями.

Две вершины, которые не принадлежат одной грани, называются противоположными.

Отрезок, который соединяет противоположные вершины, называется диагональю параллелепипеда. Соответственно у параллелепипеда есть четыре диагонали.

То есть, если в качестве оснований выбрать грани ABCDиA1B1C1D1, то боковыми гранями будут параллелограммы ABB1A1, BCC1B1, CDD1C1, DAA1D1, а боковыми рёбрами будут отрезки AA1, BB1, CC1, DD1.